负数的表示方法
计算机用二进制补码来表示有符号数,其最高位为符号位,最高位为0时为正数,为1时为负数,最大的16位正数为16#7FFF(即32767)。正数的补码是它本身,将正数的补码逐位取反(0变为1,1变为0)后加1,得到绝对值与它相同的负数的补码。将负数的补码的各位取反后加1,得到它的绝对值。例如十进制正整数35对应的二进制补码为2#00100011,十进制数-35对应的二进制数补码为2#11011101。
浮点数的表示方法
公式如下:
X = a * 2e
a为浮点数的二进制表示,范围为[1,2) ;
e为小数点移动的位数;
如:27.0表示成二进制为:11011.0,用科学计数法表示1.10110*2^4
那么如何存储1.10110*2^4这个数呢?
对于float型数据,其长度是4个字节,右边23位用来表示小数点后面的数字,中间8位用来表示e,左边一位用来表示正负。
对于double型数据,其长度是8个字节,右边52位用来表示小数点后面的数字.中间11位表示e,左边一位用来表示正负。如下图:
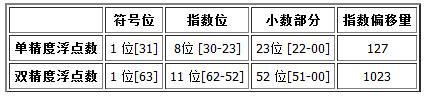
指数偏移量=2^(k-1),k为指数位个数。
因为e可以为正,可以为负数。比如1.101102^4 这个e为正数,如果是0.101那么用指数表示就是1.012^-1,那么e为-1。同时要求先把e+指数偏移量,得到的结果再化成二进制,就是我们的指数位。
小数部分:把小数点后面的数字。如上面的10110,位数不够就补零。
符号位:1表示负数,0表示正数
举例子:
27.5的二进制为11011.1
1.10111*2^4
尾数(小数点后的数)10111,补够23位 1011 1000 0000 0000 0000 000
指数:4,加上127,就是131,二进制1000 0011
用二进制表示就是 (符号数位1位)0 (指数位8位)1000 0011 (尾数位23位)1011 1000 0000 0000 0000 000
写成二进制标准形式:0100 0001 1101 1100 0000 0000 0000 0000
写成16进制就是41 DC 00 00
那么如何从二进制形式求出相应的十进制数呢?
先可以找出小数部分,指数位,以及符号位
1.通过符号位判断正负
2.算出指数位代表的十进制,把这个十进制减去指数偏移量2^(k-1),结果为正表明小数点往右边便宜e位,负则左边。
3小数部分有1,因为都有,可以不需要在计算机中存储,在这要表示出来结果是1.小数部分,如果e为正数,则把小数点往右边移动e位,负则是左边
举例子:
0x3fc00000
符号位:0 //说明是正数。
指数位:011 1111 1 //偏移0
小数位:100 0000 0000 0000 0000 0000,–>1.10000000000000000000000为1.5
而按照规定,小数点前还隐含包括1,而这个1是不储存的,所以小数位实际是1.5,当偏移大于0时,小数点向右偏移相应的值,反之向左偏移相应的值。
0x40c00000
符号位:0 //说明是正数。
指数位:100 0000 1 //偏移2
小数位:100 0000 0000 0000 0000 0000,
由于偏移为2,1.100 0000 0000 0000 0000 0000变成了110.0 0000 0000 0000 0000 0000 所以0x40c00000值为6
我们可以明白double变量的内存布局了。由于小数位的计算方式比如11.11111…在计算时为 12^1+12^0+12^(-1)+12^(-2)….可以看出在表示小数时,flaot的值不是连续的,事实上浮点数,以IEEE标准所能精确表示的仅仅是其中的一部分。